Cryptography Terminology-Basic

Cryptography

Cryptography is the study of secure communication techniques that ensure that only the sender and intended recipient of a message can view its contents.

The prefix “crypt” means “hidden” originated from greeks and suffix “graphy” means “writing”. In Cryptography, the techniques which are used to protect information are obtained from mathematical concepts and a set of rule based calculations known as algorithms to convert messages in ways that make it hard to decode it.

It is closely related to encryption, where ordinary text is encrypted into what is called ciphertext and then vice versa upon arrival. Earlier Egyptians are also known to have used these methods in their intricate hieroglyphics, and the Roman emperor Julius Caesar is credited with using one of his in one of the first modern ciphers.

The most common use of cryptography in electronic data transmission is to encrypt and decrypt emails and other plain text messages.

Uses of Cryptography:

1. Protecting user passwords
2. Secure Web Communications
3. Digital/Electronic Signatures
4. During Authentication
5. In Crypto currencies

Cryptanalysis

Cryptanalysis is a process of finding shortcomings in cryptographic algorithms and using these shortcomings to decipher the ciphertext without knowing the secret. Sometimes the weakness is not in the cryptographic algorithm itself, but rather in how it is applied that makes cryptanalysis successful.

Various types of Cryptanalysis attacks:

Known-Plaintext Analysis (KPA): In this type of attacks, several plaintext-ciphertext pairs are already known for this type of attack. Attackers map them to find encryption keys. This attack is easy to use as a lot of information is readily available.

Chosen-Plaintext Analysis (CPA) : This type of attacks involve, the attacker choosing  random plaintexts and obtaining the corresponding ciphertexts and trying to find the encryption keys. It is very simple to implement like that of KPA but the success rates are quite low.

Adaptive Chosen-Plaintext Analysis (ACPA) : This type of attack is similar Chosen-plaintext analysis attack. Here, the attacker requests the cipher texts of additional plaintexts after they have ciphertexts for some texts.

Cipher text-Only Analysis (COA) : In this type of attack, only part of the cipher text is known, so the attacker tries to find the corresponding encryption key and plaintext. This is the hardest to implement, but has the highest potential for attack since only the cipher text is required.

Birthday attack: This attack works on the probability that two or more people in a group have the same birthday. In cryptography, this type of attack is used to find hash function collisions.

Side-channel attack: This type of attack relies on information gleaned from the physical implementation of the cryptographic system rather than weaknesses in the algorithm itself. Side-channel attacks also include timing attacks, power analysis attacks, electromagnetic attacks, etc.

Differential cryptanalysis attack: This type of attack compares plaintext pairs with the corresponding ciphertext to find patterns in the encryption algorithm. May be useful for block ciphers with certain characteristics.

Man-In-The-Middle (MITM) attack: In this type of attack, an attacker intercepts messages/keys between two communicating parties over a secure channel.Brute-force attack: This attack consists of trying all possible keys until the correct key is found. While this attack is easy to implement, it can be time consuming and computationally expensive, especially for long keys.

Cryptosystems

A cryptosystem is a set of cryptographic algorithms required to implement a particular security service such as confidentiality among the CIA triad.

 A cryptosystem usually consists of three algorithms.

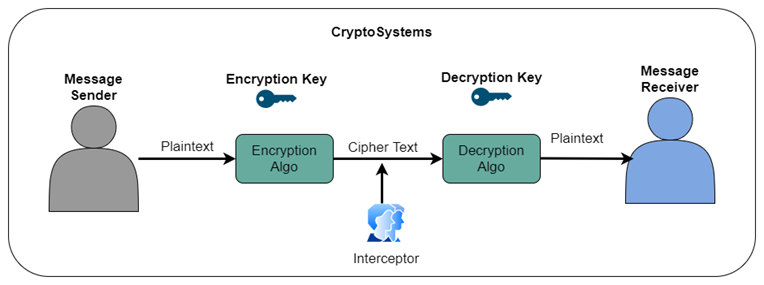
1. One for key generation,
2. One for encryption, and
3. One for decryption.

The term cipher is often used to refer to a set of algorithms, one for encryption and one for decryption. Hence, the term cryptosystem is most commonly used when key generation algorithms are important.

For this reason, the term cryptosystem is commonly used to refer to public key technology. However, both “encryption” and “cryptosystem” are used in symmetric key technology.

Cryptographic Modules

A hardware, software, or hybrid cryptographic engine confined within the boundary, along with cryptographic keys that do not cross the barrier, are used to securely perform cryptographic operations within a physical or logical boundary by a cryptographic module.

Cryptographic Strength

The phrase “cryptographically strong” is frequently used to characterize an encryption technique and suggests better resilience to attack compared to some other approach.

Not all cryptography is created equal. Some systems can be readily exploited or damaged. Others are remarkably resilient against even the most ferocious assault.

The strength of a cryptographic system refers to its capacity to defend data against intrusion.

Numerous factors affect strength, including:

1. The key’s confidentiality levels
2. The properties of the plaintext and knowledge of those properties by an attacker. (For example, a cryptographic system may be vulnerable to attack if all messages encrypted with it begin or end with a known piece of plaintext)
3. The difficulties involved in guessing every key that might work or in key searching.
4. Longer keys are typically more difficult to guess or locate.
5. The challenge of reverse engineering (or “breaking”) an encryption method without the encryption key
6. The presence (or absence) of back doors, or other techniques that make it easier to decode a file without the key.
7. The ability to decrypt an encrypted message in its whole if you know how to decrypt a portion of it (also known as a known text attack)

Cryptographic agility

Organizations utilize data encryption techniques called crypto-agility to provide a quick response to a cryptographic threat. The goal is to transition easily to a different cryptographic standard without significantly altering the infrastructure.

To secure information, cryptography employs mathematical and rule-based methods. Organizations can use crypto-agility as an additional layer of security and as an incident response tool.

When a system’s encryption algorithm is found to be weak, crypto-agility helps. Other use cases include when a security breach occurs or an algorithm unexpectedly breaks. An organization must be able to quickly transition to a new encryption technique in case one of these scenarios occurs in order to limit harm. Changes to cryptographic algorithms, security keys, certificates, and other crypto technologies are made throughout this procedure.

Without crypto-agility, a company’s cryptographic systems may be vulnerable to attack if they are compromised, which could result in a loss of revenue.

Padding

Padding in cryptography is the practice of adding text to plaintext transmissions that is of different length. Before the recipient receives the plaintext, the padding is expected to be removed. Padding has traditionally been employed to make cryptanalysis more challenging.

During encryption/decryption, plaintext data is treated one block at a time when employing block ciphers; typical block widths are 64 bits (for DES) and 128 bits (for AES). Padding is necessary because plaintext data rarely completely fills the final block. One approach is to end the last block with a 1 bit and then a string of 0 bits. If the input happens to take up a full block, a new block is introduced to make room for the padding; otherwise, the plaintext at the end of the input can be mistaken for padding. An option is stealing ciphertext. Similar to how cryptographic hash functions process input in blocks, they also need padding.

Public key cryptographic systems like RSA usually treat plaintext as a single large number in a formula. Such numbers often have to possess certain mathematical properties to avoid compromising the security of the cryptosystem, such as being even, lying within a certain range of numbers, or not being greater than 1.

Standard padding schemes such as PKCS ensure that all possible plaintexts can be turned into appropriate numbers for encryption.

Padding methods

Bit padding

In bit padding, a single ‘1’ bit is added to the message and then as many ‘0′ bits as required are added. The number of ‘0’ bits added will depend on the block boundary to which the message needs to be extended. In bit terms this is “1000 … 0000”, in hex byte terms this is “80 00 … 00 00”.

This method cannot be used to pad messages which are any number of bits long, not necessarily a whole number of bytes long.

For example, a message of 23 bits that is padded with 9 bits in order to fill a 32-bit block:

… | 1101 1011 1101 0100 0010 0111 1000 0000 |

This padding is the first step of a two-step padding scheme used in many hash functions including MD5 and SHA. In this context, it is specified by RFC1321 step 3.1.

In the context of using block ciphers to process variable-size messages, this padding scheme is known as ISO/IEC 9797-1 Padding Method 2.

Byte padding

ANSI X.923

In ANSI X.923 padding, bytes are filled with zeros (0)’s are padded and the last byte defines the padding boundaries or the number of padded bytes.

Example: In the following example the block size is 8 bytes, and padding is required for 4 bytes (in Hexadecimal format)

... | DD DD DD DD DD DD DD DD | DD DD DD DD 00 00 00 04 |

PKCS#5 and PKCS#7 Padding

The value of each pad byte is the total number of bytes that are added. Of course, the total number of pad bytes depends on the block size.

For example, if the message is 3 bytes shorter than an integer multiple of the block size, then 3 pad bytes should be added, each of them of value 3. If 5 bytes should be added, then each of them should be 5.

0x10 0x11 0x36 0x67 0x38 0xBC 0x03 0x21 0xEF  0x03 0x03 0x03
0x10 0x11 0x36 0x67 0x38 0xBC  0x06 0x06 0x06 0x06 0x06 0x06

Nonce

A nonce is a number that is used in cryptography to safeguard private communications by thwarting replay attacks.

Nonces are numbers that authentication protocols use to tack on randomness or pseudo-randomness to communications. To emphasize the momentary character of these communications, these figures occasionally carry a timestamp. Subsequent requests to a server are denied if they contain the incorrect nonce and/or timestamp, as can happen, for instance, during digest access authentication with a username and password. Nonces can stop replay attacks that rely on imitating earlier communications to obtain access when utilized in this fashion.

Replay attacks can be avoided by using a nonce in an authentication protocol, which ensures that previous messages are not reused. The nonce aids in establishing the sender identity of the message and prevents malicious parties from intercepting and resending it. A nonce should have both sequential and random components in order to be optimized.

Usage scenarios

1. Initialization: In data encryption, an initialization vector is a nonce since it is usually arbitrary or pseudo-random and only used once during a session.
2. During authentication: In HTTP digest access authentication, the password’s MD5 digest can be computed using a nonce. The nonce will vary with each 401 authentication challenge response code that is sent out. To make sure that online shopping transactions are legitimate, this is extremely helpful. By using a nonce for authentication, it is possible to prevent the processing and reuse of previous communications. To stop a bad actor from exploiting the first order to place additional orders using the client’s details, an e-commerce site, for instance, can append a nonce to each transaction made by a customer.
3. In asymmetric Cryptography: When two distinct nonce values are generated and exchanged during the SSL/TLS (secure socket layer/transport layer security) handshake, nonce values can be utilized in public-key cryptography. A distinct nonce value will be created by the client and the server and verified using a private/public key pair.

Salting

Generally, passwords are not stored in cleartext, but rather hashed.

The attackers can simply generate a list of common passwords and their corresponding hashes. Comparing the hashes that a site has stored with the table will, if common passwords are being used, reveal the passwords to the attacker.

To make a password hash result unique even for users using common passwords, a salt is only applied. The idea behind it is to render pre-computation based attacks useless. Any pre-computed password-hash table targeting unsalted password hashes or targeting an account with a different salt will not help in cracking your account’s password if your password is stored with a unique salt. Salts can therefore be utilized to completely render pre-computational attacks useless.

The hash value recorded in the database is Hash(salt||password), which is the easiest way to combine the salt and the password. The typical password password1 now suddenly transforms into something that is unlikely to be in a password cracker’s table, such as 6$qK,4gCA%Jpassword1.

In the database, adjacent to the hashed value, the salt can be kept totally in the open. The pre-calculated table for each salt must be generated separately, which is an expensive process, once the attacker gets access to the database and wants to find the passwords.

Password stretching, or making a password hash more difficult to compute for everyone, including the log-in service and password crackers, is another method to assist defend against offline password cracking. Iterating the hash function several times, i.e. storing Hash(Hash(Hash…(Hash(salt||password)))…), is one technique used to stretch passwords.

The term “pepper” refers to yet another prevalent salt-related concept. In other words, the password is combined with a different random value, resulting in the stored value Hash(pepper||salt||password). The pepper is then not kept at all in storage. It takes longer for both the login server and password cracker to compare password hashes because they both need to use brute force to find the unknown pepper value.

One-time pad

The perfect cipher, commonly known as the Vernam cipher or the one-time pad (OTP), is a cryptographic technique that combines plaintext with a random key. It is the only encryption that is currently mathematically impenetrable.

The one-time pad developed a reputation as a straightforward but reliable encryption technique with absolute security that cannot be equaled by the current generation of cryptographic algorithms. One-time pad encryption is and will remain the only genuinely impenetrable technology that offers genuine long-term message secrecy, regardless of future technological advancements.

One-time pads are effective only if a few key guidelines are met. The one-time pad can be shown to be impenetrable if these guidelines are followed correctly.

Because it is mathematically impossible, one-time pad encryption cannot be broken even with unlimited processing power and time.

However, if only one of these guidelines is broken, the cipher can no longer be cracked.

• The key is actually random—it wasn’t created by some easy computer procedure or something similar.
• The length of the key is at least equal to that of the message or data being encrypted.
• Calculations of the key and plaintext are done modulo 10 for digits, modulo 26 for letters, or modulo 2 for binary.
• The sender and the recipient should each have their own copy of the key; there are some exceptions for multiple receivers.
• Each key can only be used once, and the sender and the recipient both have to destroy their keys after usage.

Checksum

Checksum is a numerical value generated after a cryptographic algorithm has been applied to a message/file which will be sent across a network. It is used to make sure that the message/file hasn’t been altered.

The cryptographic algorithm applies a number of mathematical operations to create a hash value, or fixed string of digits. This generated hash value is then used as a checksum to verify that the sent file was not changed by an attacker.

Modern cryptography, particularly for signing and encryption, digital signatures, email certificates, and website certificates, is built on cryptographic checksums. They are also known as message integrity codes, modification detection codes, integrity check values, or message authentication codes.

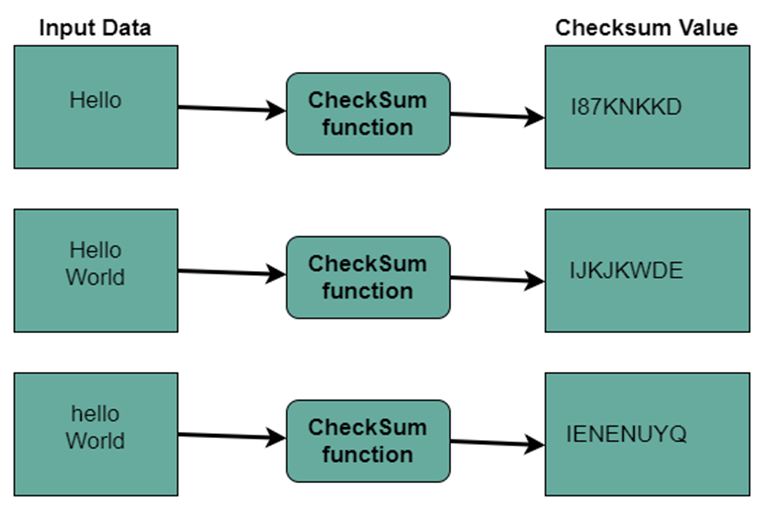
Using a cryptographic checksum involves the following steps:

1. The checksum is generated from the message, which is then sent to a destination computer.
2. The checksum is then encrypted and sent to the destination computer, which receives both the message and the checksum.

• The checksum is then decrypted.

• The destination computer then recalculates the checksum using the received message and compares it with the decrypted value of the checksum that has been received. If the two checksums match, there is a high likelihood that the message was sent successfully.

• If the two checksums match, then there is a high probability that the message has not been tampered with.

Following are a few checksum algorithms:

MD5, SHA-1, SHA-256 and SHA512

Uses of cryptographic checksums:

1. Maintaining file integrity
2. Storing passwords
3. Email archiving
4. Images ownership

PRNG

Programmers became aware of the necessity for a way to include randomness into a computer program with the invention of computers. Even though it may appear surprising, it is challenging to persuade a computer to act in an unpredictable way because it blindly obeys all commands and is thus entirely predictable. A technique called PRNG was created to produce random numbers using a computer since it is impossible to produce truly random numbers from predictable objects like computers.

A pseudo-random number generator (PRNG) is a technique that generates random number sequences using mathematical formulas. A series of numbers that closely resemble the characteristics of random numbers are produced by PRNGs. A seed state is used by a PRNG to start from any starting state. If the beginning of the series is known, many numbers are created quickly and can also be repeated later. As a result, the numbers are accurate and deterministic.

A PRNG is a deterministic process, which means that if it were to be put back in the same condition or be initialized with the same seed, it would recreate the same sequence. Because of this characteristic, PRNGs can be used as stream ciphers. PRNGs are helpful for applications where a large set of  random numbers are required and where it is useful that the same sequence can be replayed easily.

Also Read: Terminology-Intermediate, Terminology-Advanced, Security Terminology Section

Suggested Exercises: Cryptography Tests